Faculté des Sciences Appliquées	Projet 2 Version 1 du 10.10.2011
Mécanique Rationnelle 2^èmebachelier 2011-2012		Pendule avec Ressort

Comment procéder pour télécharger et utiliser la démo ?

Version compilée avec Matlab2004 et qui fonctionne sous Windows XP (testé le 10-10-2011)

- Télécharger et installer MCRInstaller.exe qui contient des librairies (si Matlab est déjà installé,exécutez le MCRInstaller.exe qui est livré avec Matlab)

- Télécharger projet2gui.exe

- Télécharger projet2gui.ctf (si votre browser force l’extension .zip, transformez-la en .ctf)

Les fichiers projet1gui.exe et projet1guide.ctf doivent se trouver dans un même répertoire.

Ci-après une copie écran de l’exécutable en question.

Pour tout souci : cfao.matlab@ulb.ac.be

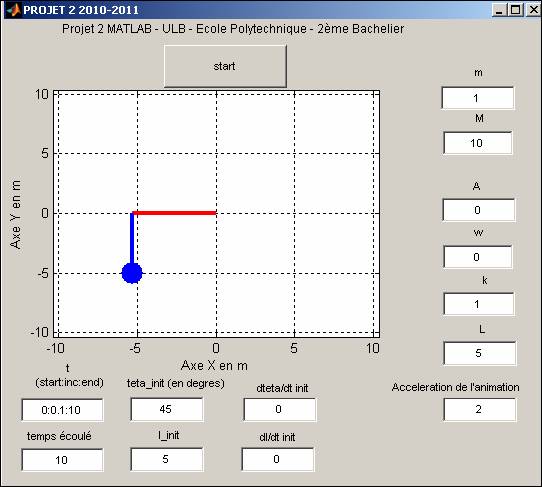
1.

Un pendule est constitué d’une masse ponctuelle m à l’extrémité d’une barre sans masse de longueur l. L’autre extrémité de cette barre estattachée à une masse ponctuelle M qui peut se mouvoir horizontalement et qui est solidaire d’une ressort de longueur nulle au repos et de constante de rappel k. Ce ressort peut s’étendre indifféremment dans les deux sens. L’extérmité du ressort non solidaire de la masse M peut avoir un mouvement imposé A.sin(wt) On demande 1. d’écrire les équations du mouvement en fonction des paramètres m, M, k, A et w 2. d’écrire la valeur de l’energie du système. Est-elle constante ? 3. d’étudier avec Matlab le mouvement en faisant varier les paramètres m, M, k en considérant A =0 4. d’étudier avec Matlab le mouvement en faisant varier les paramètres m, M, k en considérant A différent de 0

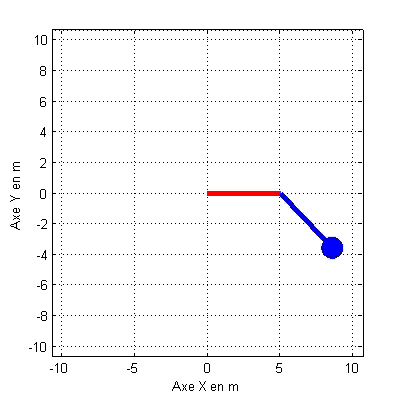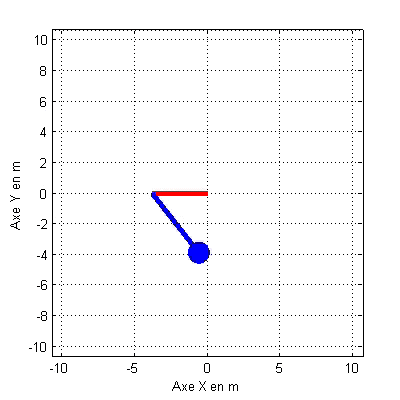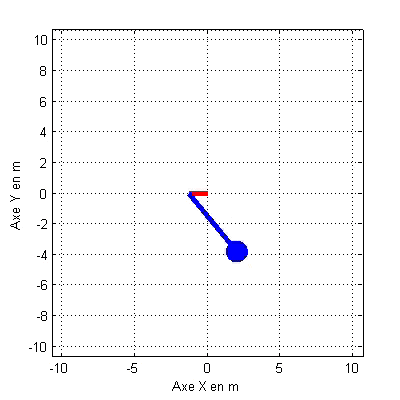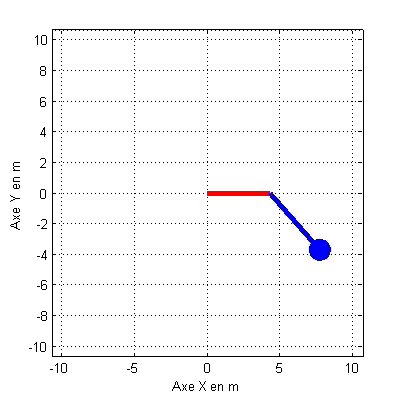
Cas : k = 1;l=5 ;x(0) = 5; dx/dt(0)=0 ;m = 1;M = 10;w = 0;A = 0 ; q (0)=45° ;dq/dt(0)=0 ;

Pour ceux qui le souhaitent, voici une tactique parmi d’autres pour progresser dans le projet :

Vous verrez - lors des séminaires matlab - 4 outils : l’évolution de la solution (position et vitesse) en fonction du temps, le plan des phases (la vitesse en fonction de la position), la section de Poincaré depuis le plan des phases (la vitesse en fonction de la position échantillonnée), et le diagramme des bifurcations.

Commencez par l’évolution en fonction du temps pour voir si le mouvement vous semble périodique ou en transition vers le chaos (doublement, triplement de période). Utilisez le critère (condition nécessaire) de sensibilité aux conditions pour confirmer/infirmer votre intuition. Le plan des phases vous permet aussi d’y voir clair et même de trouver d’autres phénomènes à côté du chaos. Un mouvement périodique sera une courbe fermée (différente selon la condition initiale). Un cycle limite (un mouvement stationnaire de type régime) sera une courbe vers laquelle la trajectoire tendra toujours quelle que soit la condition initiale. Si l’équation ne dépend pas du temps, la courbe ne se coupera jamais dans le plan des phases. Toujours dans le cas où il n’y a pas de dépendance explicite par rapport au temps, quelle que soit la condition initiale, la courbe dans la plan des phases correspondante à une condition initiale ne coupera jamais une autre courbe correspondant à une autre condition initiale.

Vous pensez avoir trouvé des valeurs de paramètre qui donnent un mouvement chaotique ? Confirmez avec une section de Poincaré en jouant sur la période d’échantillonnage pour améliorer l’esthétique de la section de Poincaré (qui doit être, dans le cas d’un mouvement chaotique, une courbe fractale).

Dans une zone à chaos, certaines conditions initiales peuvent donner lieu à un mouvement chaotique, d’autres pas. Si vous superposez les sections de Poincaré correspondantes à ces conditions initiales, vous verrez immédiatement la différence.

Quand vous avez suffisamment balayé les valeurs des paramètres, résumez le tout sur un diagramme de bifurcations qui peut être vue comme une projection sur l’axe y de la section de Poincaré pour différentes valeurs du paramètres.

En conclusion, utilisez donc les 4 outils suivants : :

Outil n°1 : Evolution en fonction du temps est un grahe (t, x(t))) ou dx/dt(t))

Outil n°2 : Plan des phases est un graphe : (x(t), dx(t)/dt

Outil n°3 : Section de Poincaré est un graphe : : (x(T), dx(T)/dt où, par exemple,T=2.p/w

Outil n°4: Diagramme de bifurcation : (A.w², x(T))

Comme votre projet est à deux ddl, vous pouvez limiter l’utilisation des outils à un seul de ces degrés de liberté. Les deux degrés de liberté étant couplé, ce que vous trouverez en terme de section de Poincaré, plan des phases, diagramme de bifurcation sur un des degrés de liberté vaudra pour l’autre (du moins qualititivement).

Ceci dit, il se peut que vous soyez dans une configuration des paramètres et une modélisation qui ne donne pas de chaos. Dans ce cas, convainquez le lecteur que vous avez tout essayé pour le trouver.

Vous êtes perdu devant la quantité de paramètres à tester ?

Utilisez votre fibre ingénieur ! Commencez par tester les valeurs des paramètres dont vous pouvez dire que vous y avez le plus facilement accès. S’il est question dans votre projet d’un mouvement forcé, on peut considérer qu’il s’agit d’un moteur pour lequel vous pouvez facilement modifier A ou la vitesse angulaire w.

Ensuite tester les valeurs de k en prenant des valeurs réalistes. Un ressort que vous pouvez presser à la main fait k=quelques centaines de N/m. Un ressort que vous devez comprimer avec tout le poids de votre corps fait quelques milliers de N/m. Testez donc ces fenêtres (ne négligeant pas non plus des valeurs plus petites ou plus grandes).

Enfin, testez si l’amortissement change les conclusions que vous aurez trouvées.

Depuis le 10.10.2011, vous êtes le visiteur n° : 40