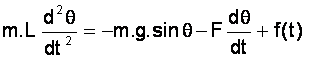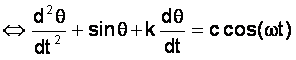Faculté des

Sciences Appliquées

Mécanique Rationnelle

2^èmebachelier 2010-2011

Complément Séminaire 29-10-2010

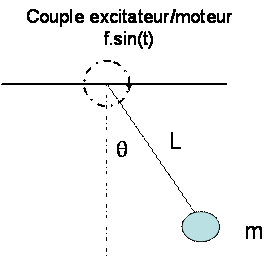
Soit un pendule simple constitué d’une barre rigide de longueur L sans masse et une masse pesante ponctuelle m attachée à son extrémité.

Le pendule soumis à une friction proportionnelle à sa vitesse de rotation : dq/dt.
Le pendule soumis à une force excitatrice périodique f(t).

Exemple d’un pendule qui répond à cette équation :

Equation du movement:

global c w k

c=1.65;

k=0.5;

w=2/3;

figure('NumberTitle','on','Name','SCI','Renderer','OpenGL','Color','w','Position',[100 100 600 600])

box on;

hold on

options = odeset('RelTol',1e-4);

[t1,teta1] = ode45('duffing_eq',[0:0.25:150],[0 0],options);

[t2,teta2] = ode45('duffing_eq',[0:0.25:150],[0.01 0],options);

for i=2:max(size(t1))

tic

subplot(2,1,1,'replace')

box on;

title(['Pendule Duffing - k=',num2str(k),' Terme forcé c =',num2str(c)]);

xlabel('X [unités de longueur arbitraire]');

ylabel('Y [unités de longueur arbitraire]');

axis([-60 60 -20 20])

line([0 9.81*sin(teta1(i,1))],[0 -9.81*cos(teta1(i,1))],'LineWidth',2);

line([0 9.81*sin(teta2(i,1))],[0 -9.81*cos(teta2(i,1))],'LineWidth',2,'Color','r');

line([ 9.81*sin(teta1(i,1))],[ -9.81*cos(teta1(i,1))],'Marker','.','Markersize',40);

line([ 9.81*sin(teta2(i,1))],[ -9.81*cos(teta2(i,1))],'Marker','.','Markersize',40,'Color','r');

subplot(2,1,2)

box on;

xlabel('t [s]');

ylabel('\theta [degrés]');

line([t1(i-1) t1(i)],[teta1(i-1)*180/pi teta1(i)*180/pi],'LineWidth',2);

line([t2(i-1) t2(i)],[teta2(i-1)*180/pi teta2(i)*180/pi],'LineWidth',2,'Color','r');

line([t1(i-1) t1(i)],[30*c*cos(w*t1(i-1)) 30*c*cos(w*t1(i))],'LineWidth',2,'Color','k');

while toc<0.025;end

drawnow;

end;

function dy = duffing_eq(t,y)

global c w k

dy = zeros(2,1);

dy(1) = y(2);

dy(2) = -k*y(2)-sin(y(1))+c*cos(w*t);

code pour la section de poincaré

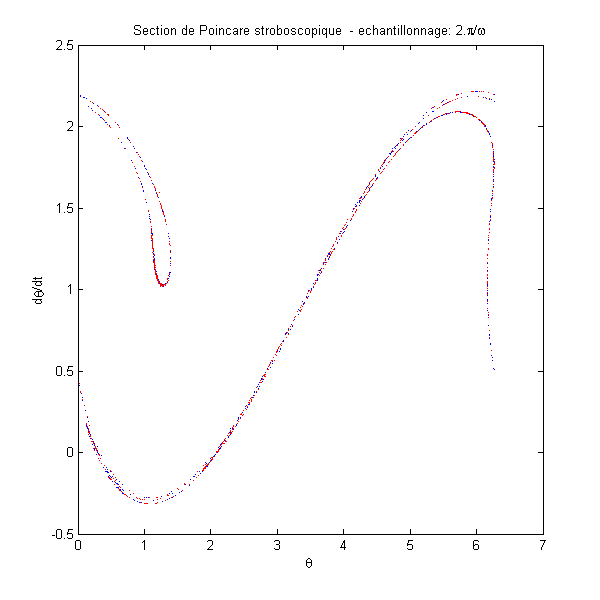
global c w k

c=1.2;k=0.5;w=2/3;

figure('NumberTitle','on','Name','SCI','Renderer','OpenGL','Color','w','Position',[100 100 600 600])

box on;

hold on

options = odeset('RelTol',1e-4);

[t1,teta1] = ode45('duffing_eq',[0:2*pi/w:100000],[0 0],options);

[t2,teta2] = ode45('duffing_eq',[0:2*pi/w:100000],[0.01 0],options);

plot(mod(teta1(1000:10:end,1),2*pi),teta1(1000:10:end,2),'.','Markersize',1)

plot(mod(teta2(1000:10:end,1),2*pi),teta2(1000:10:end,2),'.','Color','red','Markersize',1)

title('Section de Poincare stroboscopique - echantillonnage: 2.\pi/\omega')

xlabel('\theta')

ylabel('d\theta/dt')

Cas c=1.2-k=0.5-w=2/3

Cas c=0.5-k=0.5-w=2/3

Cas c=1.65-k=0.5-w=2/3

Bifurcations

Cas c=1.2;k=0.5;w=2/3;

La position initiale entre le pendule rouge et bleu diffère de 1/100 radians.

Après un temps fini, les deux mouvements divergent et il est clair que les deux mouvements sont chaotiques.

CHAOS

Evolution temporelle

Plan des phases

Section de Poincaré

Evolution temporelle et plan des phases

↑↑ haut ↑↑

Section de Poincaré

↑↑ haut ↑↑

Cas c=0.5;k=0.5;w=2/3;

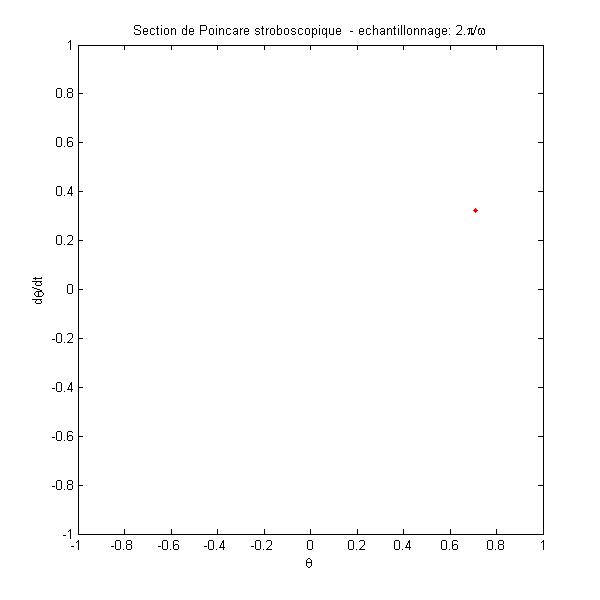
La position initiale entre le pendule rouge et bleu diffère de 1/100 radians.

Les mouvements restent confondus et le mouvement n’est clairement pas chaotique. La période du mouvement est identique à celle de l’excitation.

MOUVEMENT PERIODIQUE

Evolution temporelle

Plan des phases

Section de Poincaré

Evolution temporelle et plan des phases

↑↑ haut ↑↑

Section de Poincaré

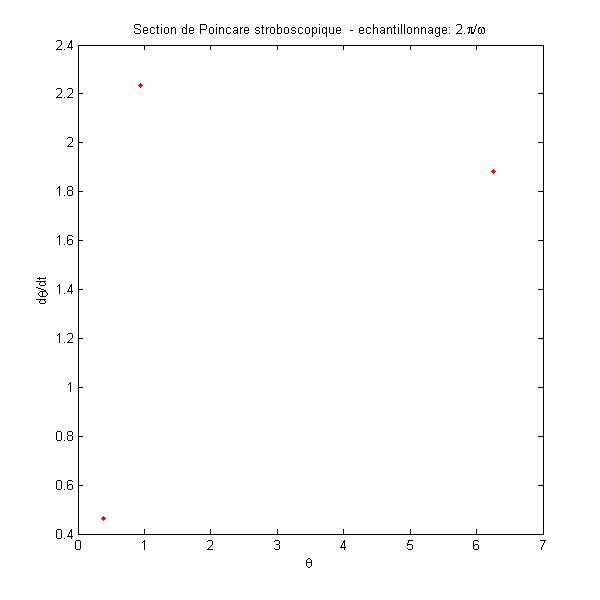
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE
IMAGE LONGUE A CHARGER - PATIENCE

↑↑ haut ↑↑

Cas c=1.65;k=0.5;w=2/3;

Le mouvement reste périodique mais la période n’est plus la même que l’excitation (visualisé par la courbe noire).

C’est un signe de transition vers le chaos.

TRANSITION VERS LE CHAOS

Evolution temporelle

Plan des phases

Section de Poincaré

Evolution Temporelle et Plan des Phases

Noter le n-umplement de la période de la réponse par rapport à la période excitatrice (courbe noire magnifiée quelques dizaines de fois). C’est un indice de transition vers le chaos.

↑↑ haut ↑↑

Section de Poincaré

↑↑ haut ↑↑

Diagramme de bifurcations

fig1=figure('Name','Diagrammes de bifurcations - Pendule forcé');

fig2=figure('Name','Diagrammes de bifurcations - Pendule forcé - CI: (0,0)');

fig3=figure('Name','Diagrammes de bifurcations - Pendule forcé - CI: (0,1)');

fig4=figure('Name','Diagrammes de bifurcations - Pendule forcé - CI: (0,2)');

global c w k

k=0.5;

w=2/3;

for c=0.9:0.01:2

for i=0:2

clear y

options = odeset('RelTol',1e-4);

[t,y] = ode45('bifurcation_diagramme_eq',[0:1*2*pi/w:1*2*pi/w*50],[0 i],options);

if i==0

figure(fig1)

plot(c,y(30:50,2),'rs','Markersize',2);

hold on

figure(fig2)

plot(c,y(30:50,2),'rs','Markersize',2)

hold on

end

if i==1

figure(fig1)

plot(c,y(30:50,2),'bs','Markersize',2);

hold on

figure(fig3)

plot(c,y(30:50,2),'bs','Markersize',2)

hold on

end

if i==2

figure(fig1)

plot(c,y(30:50,2),'gs','Markersize',2);

hold on

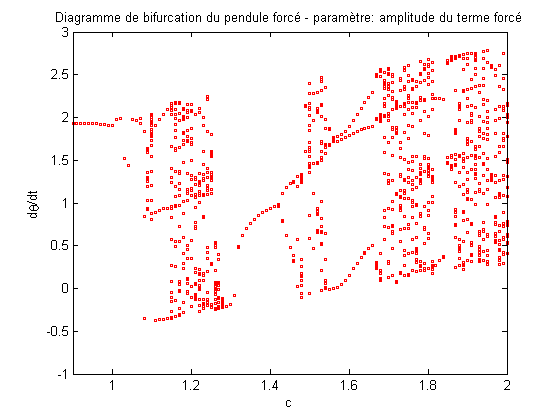
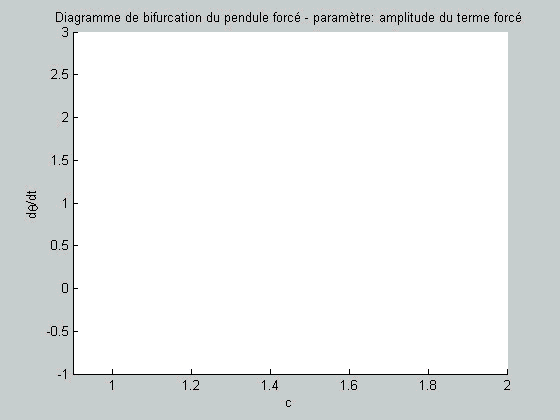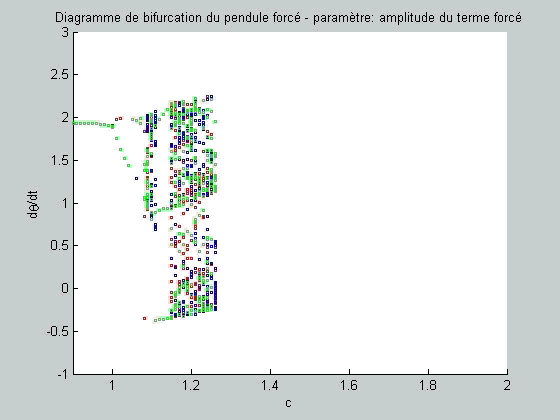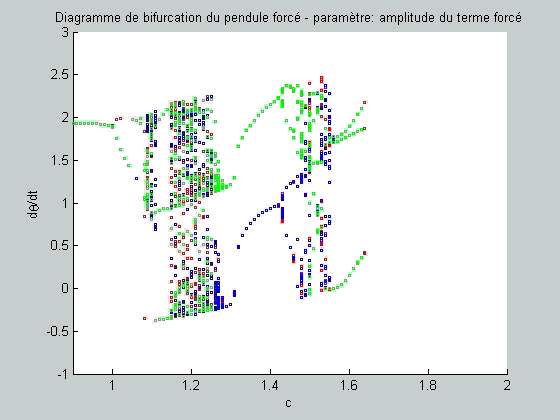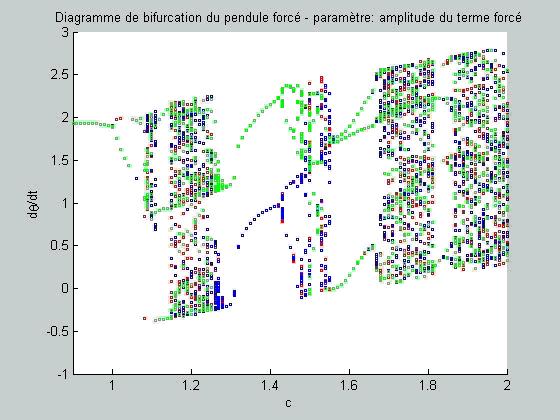
figure(fig4)

plot(c,y(30:50,2),'gs','Markersize',2)

hold on

end

figure(fig1);

axis([0.9 2 -1 3])

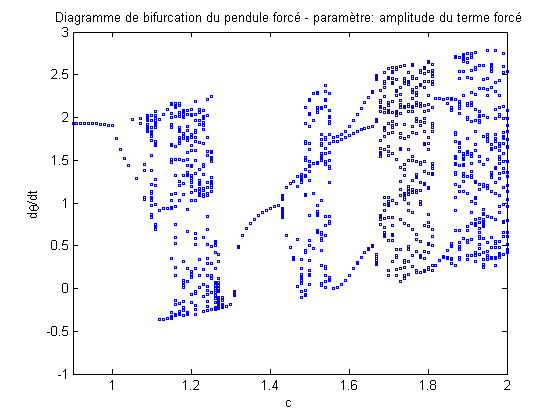
title('Diagramme de bifurcation du pendule forcé - paramètre: amplitude du terme forcé');

xlabel('c');

ylabel('d\theta/dt');

figure(fig2);

axis([0.9 2 -1 3])

title('Diagramme de bifurcation du pendule forcé - paramètre: amplitude du terme forcé');

xlabel('c');

ylabel('d\theta/dt');

figure(fig3);

axis([0.9 2 -1 3])

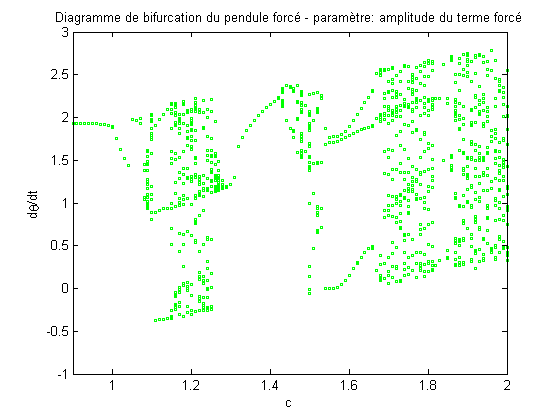
title('Diagramme de bifurcation du pendule forcé - paramètre: amplitude du terme forcé');

xlabel('c');

ylabel('d\theta/dt');

figure(fig4);

axis([0.9 2 -1 3])

title('Diagramme de bifurcation du pendule forcé - paramètre: amplitude du terme forcé');

xlabel('c');

ylabel('d\theta/dt');

function dy = bifurcation_diagramme_eq(t,y)

global c w k

dy = zeros(2,1);

dy(1) = y(2);

dy(2) = -k*y(2)-sin(y(1))+c*cos(w*t);

Depuis le 18.10.2010, vous êtes le visiteur n° : 1,159